深度学习Review【一】线性回归、Softmax、感知机、卷积
一、线性回归
线性模型:y = ax + b
单层神经网络(输出层不看做是一层)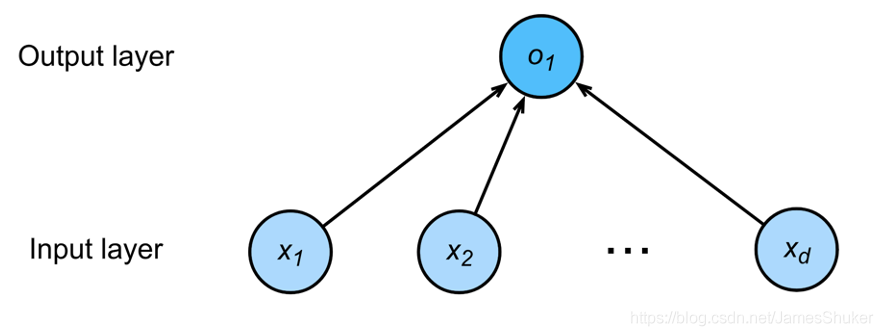
1 损失函数
比较真实值和预估值
以下几种损失函数比较
- 0-1损失函数(zero-one loss)
- 绝对值损失函数
- log对数损失函数
- 平方损失函数
- 指数损失函数(exponential loss)
- Hinge 损失函数
- 感知损失(perceptron loss)函数
- 交叉熵损失函数 (Cross-entropy loss function)
2 参数学习
选取不同的w和b,根据输入X,计算y的损失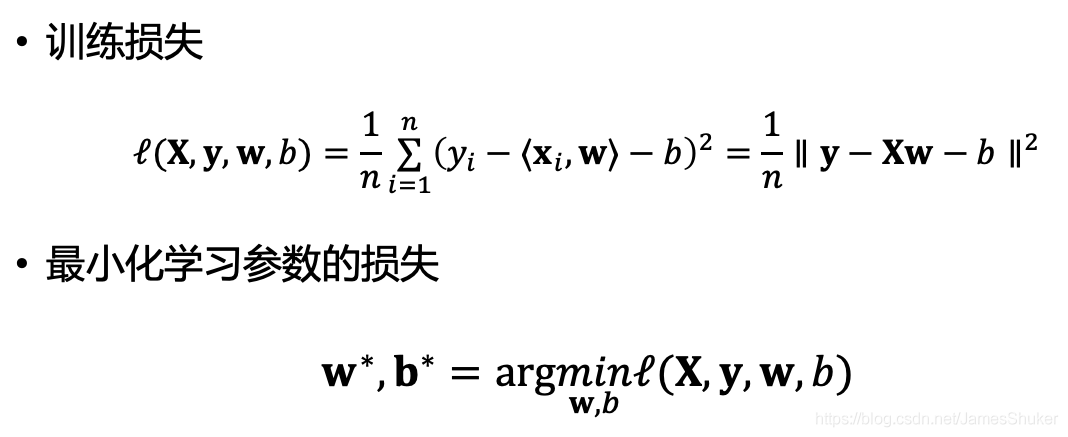
3 梯度下降 GD

学习率:每次计算loss后调整的步长
小批量随机梯度下降 SGD:通过随机采样b个样本计算近似损失,以减少计算梯度求导的消耗
这里的b 就是batchsize,并行进入神经网络的样本数量
3 torch实现
# `nn` 是神经网络的缩写
from torch import nn
#Sequential是存放网络的list
#全连接层(单层网络)输入维度是2 输出为1
net = nn.Sequential(nn.Linear(2, 1))
#初始化网络参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
#损失函数 均方误差
loss = nn.MSELoss()
#定义优化算法 小批量随机梯度下降 传入net的参数w和b 指定学习率lr
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
#训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad() #梯度清零以计算backward
l.backward()
trainer.step() #更新模型
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)二、Softmax分类
预测离散的类型,通常有多个输出,输出 i 是预测为第 i 类的置信度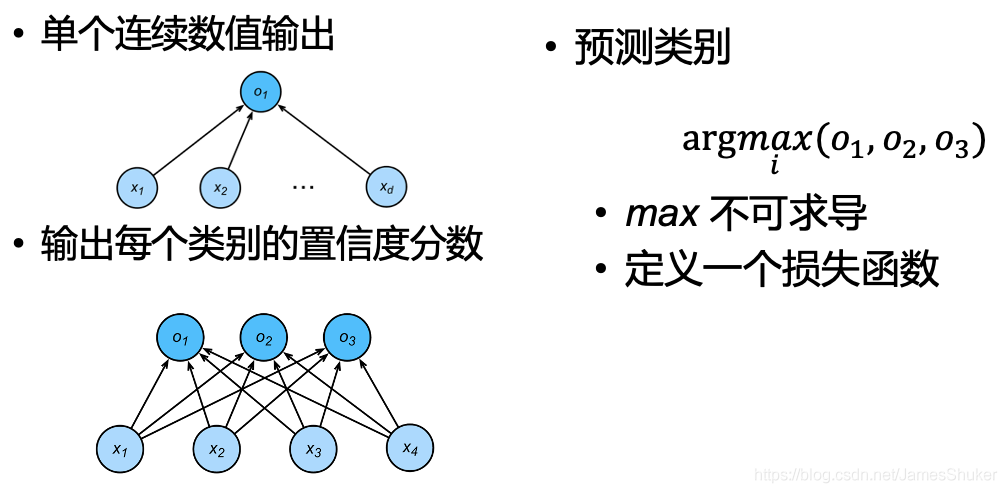
对每个类别进行一位有效编码(==One-Hot==),编码后为向量y作为输入,每个类别的置信度分数(即每个类别的概率)作为输出(输出向量的每个元素非负,元素和为1)
使用均方损失函数训练
1 损失函数
橙色为导数,绿色为最大似然函数,蓝色为损失函数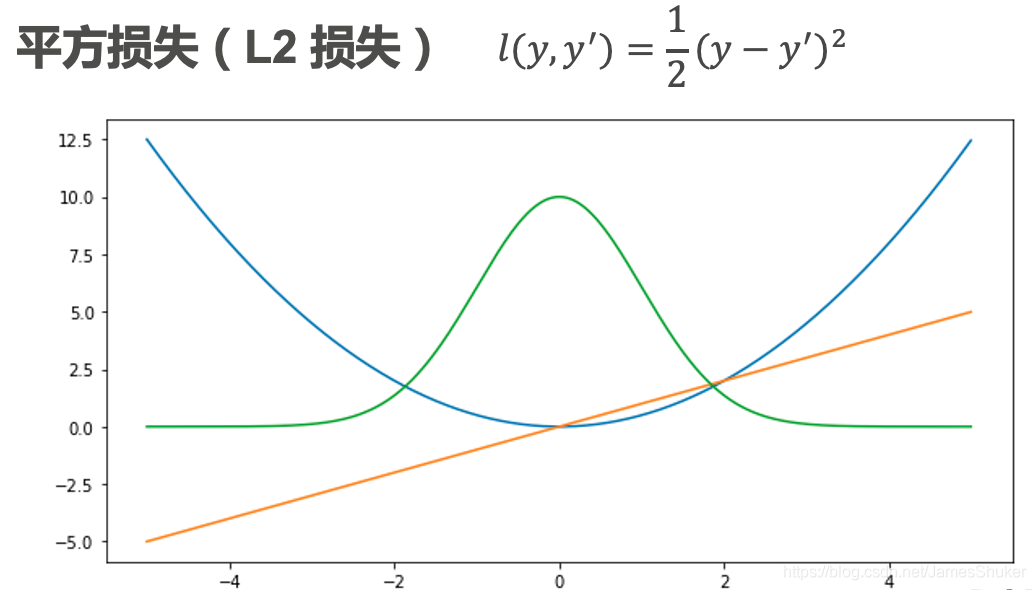
随着预测值和真实值相差不同,进行不同的优化
不管预测值和真实值相差多远,都能稳定优化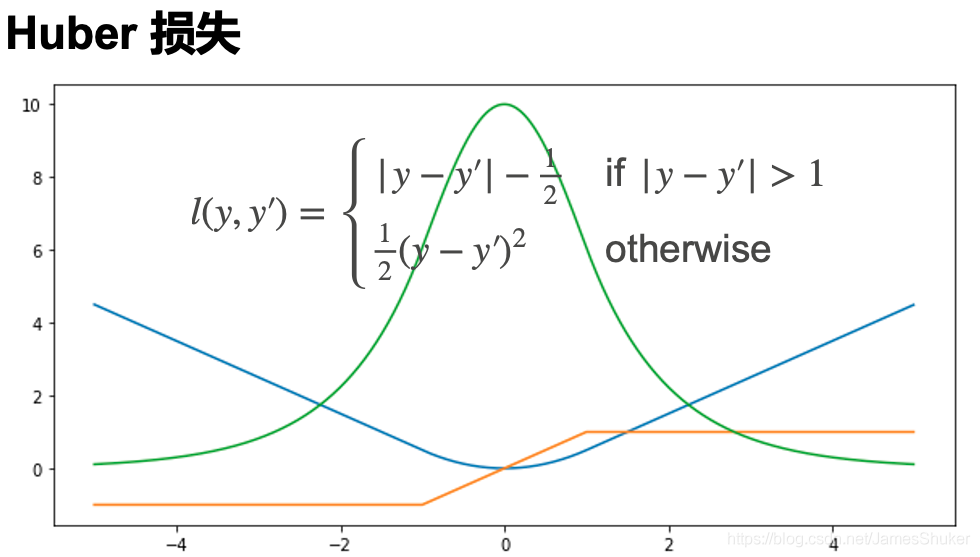
在预测值和真实值相差不大时,减少优化
2 torch实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# PyTorch不会隐式地调整输入的形状 在线性层前定义展平层(flatten)调整网络输入的形状
#输入为784 输出为10
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
#初始化为均值为0方差为0.01的随机值
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
#训练模型
num_epochs = 10
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)三、感知机 Perceptron
1 二分类的感知机
二分类问题,x为给定输入,w为权重,b为偏移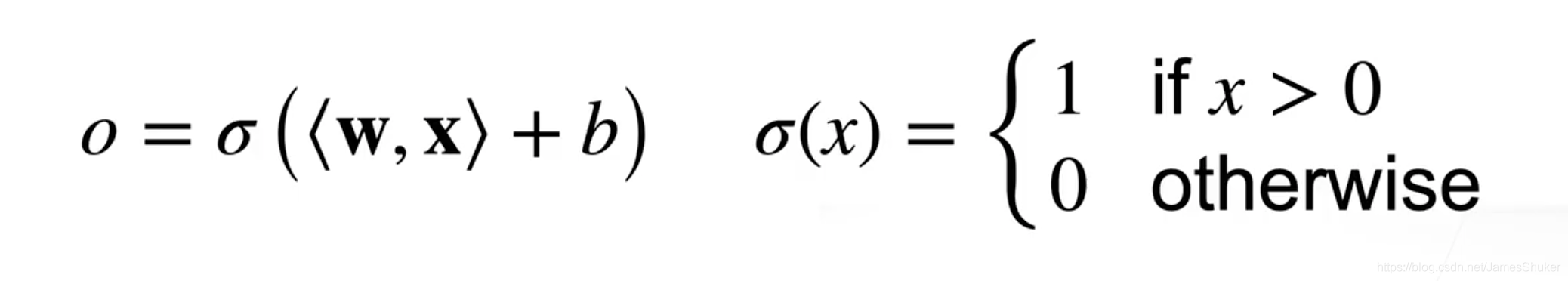
线性回归输出的是实数,softmax回归输出的是概率,这里只输出0和1(或者-1和1)是二分类问题
y为实际值,wx+b为预测值,以下所有wx为w和x的混合积
w=b=0;
while(所有分类正确):
if (y*[wx+b]<=0) w+=y*x,b+=y;等价于使用batchsize为1的梯度下降,其中loss=max(0,-y*wx)
根据收敛定理,对于正确的数据一定可以得到一条直线,将两类样本点分开
局限:普通感知机不能拟合XOR函数,必须使用多层感知机
2 多层感知机MLP
两个分类器做乘法(用与门和或门实现与或门)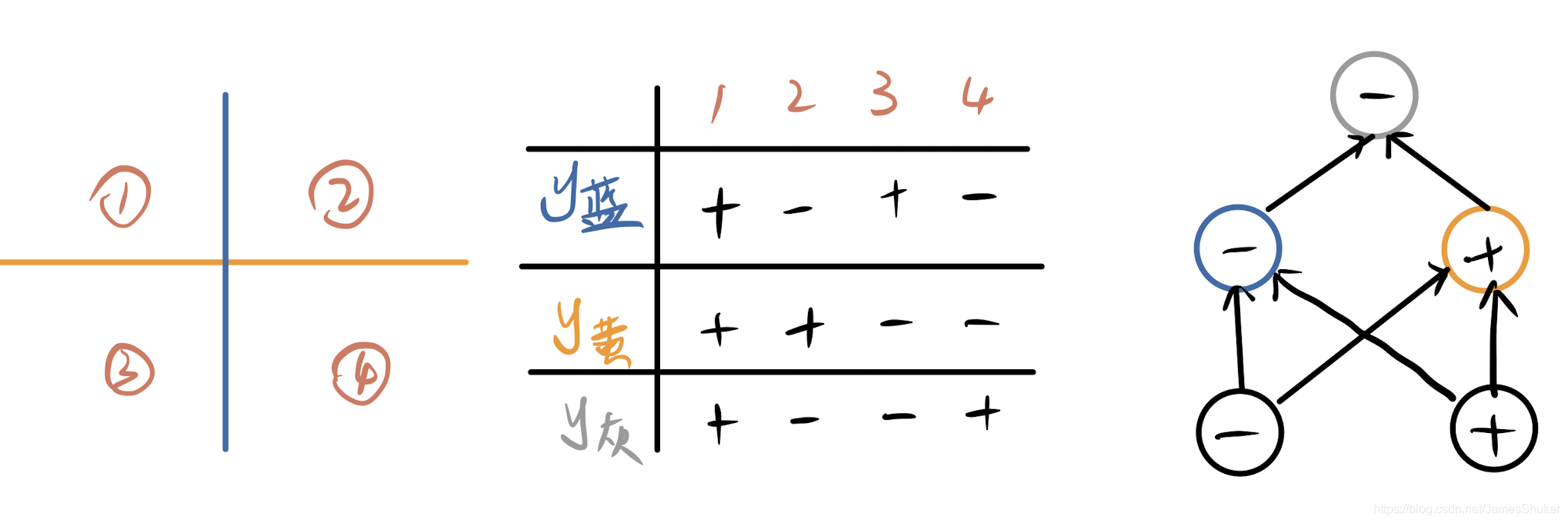
单隐藏层-单分类
Hidden-layer隐藏层是 mxn 的矩阵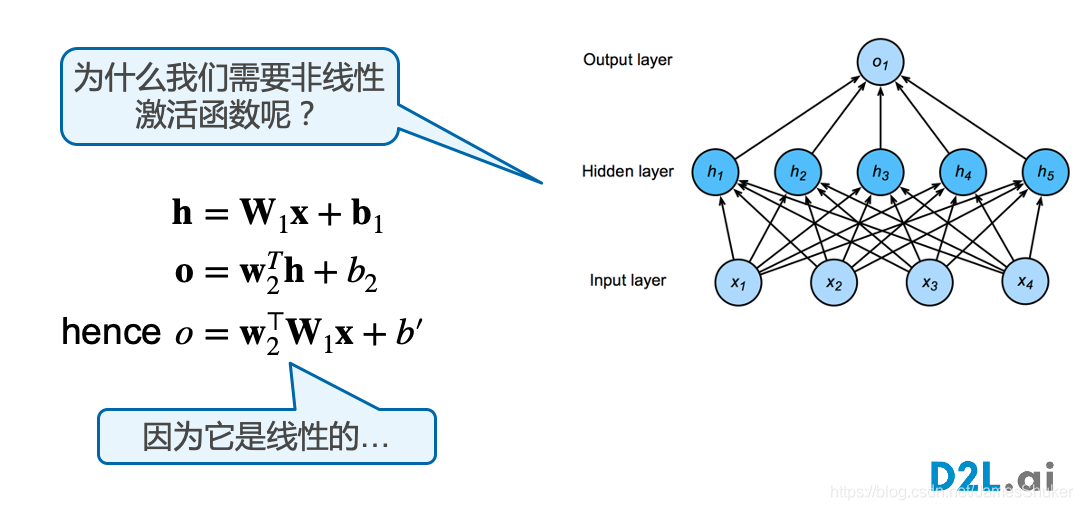
使用线性==激活函数==会导致多个连接层摞在一起,变成单层感知机;应当使用Sigmoid、Tanh、ReLU
多隐藏层多分类
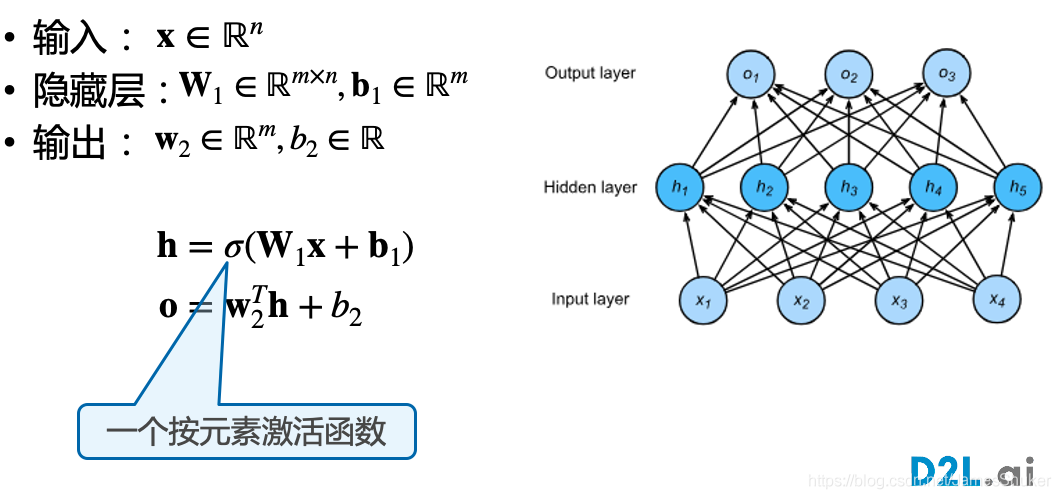
结果 y = ==softmax== (o)
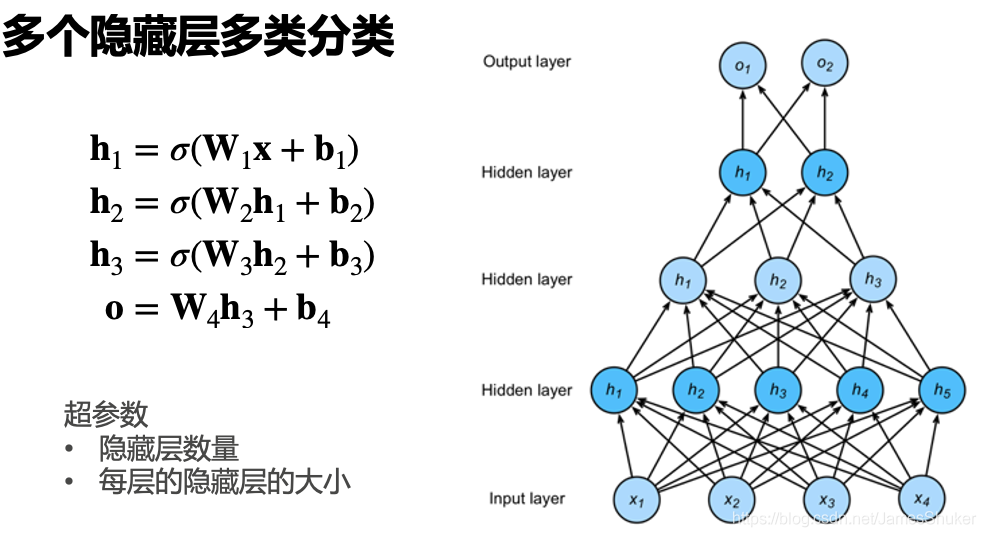
每次计算出隐藏层结果之前都要使用非线性激活函数,最后一层可以直接通过softmax得到y
3 torch实现
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
# 将三维flatten成二维
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()#交叉熵损失
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)四、卷积层
1 卷积操作
卷积是具有平移不变性(权重共享)和局部性的全连接
以下以二维卷积为例
二维交叉相关:w为权重,v为重新构建索引后的w
平移不变性:换不同的位置 卷积的计算方式不改变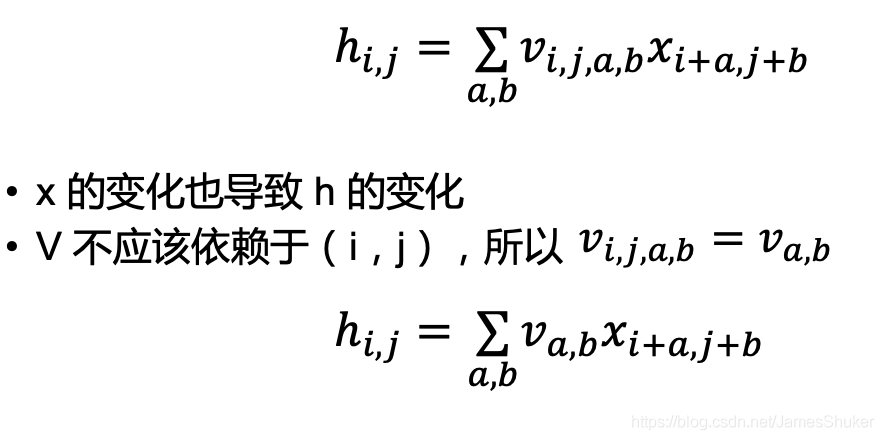
局部性:卷积核在局部进行运算即可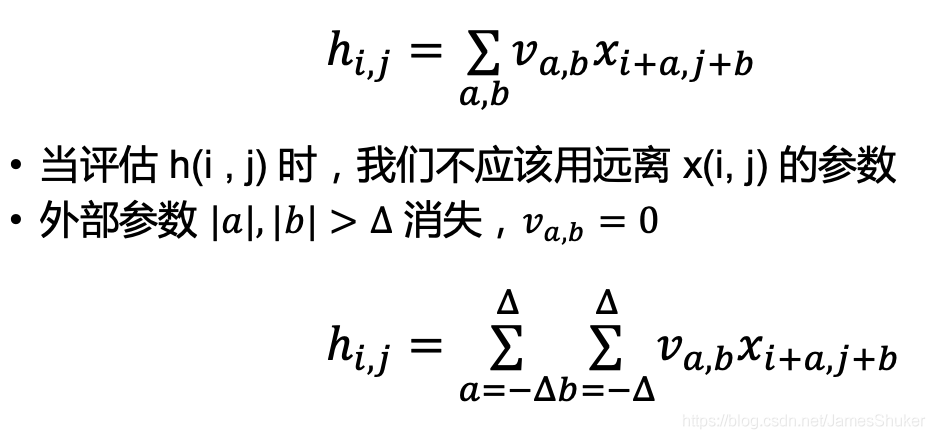
2 卷积层

填充:通过填充保证卷积后矩阵尺寸不会太小
步长(步幅):矩阵太大,跳过一些以控制输出
3 gif
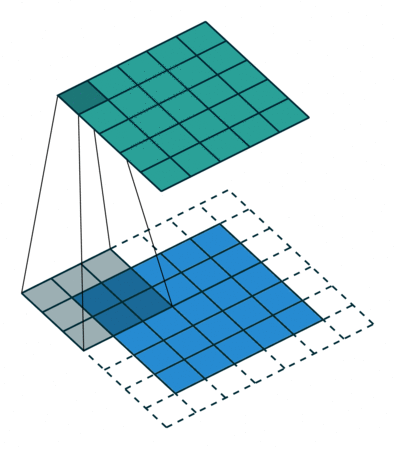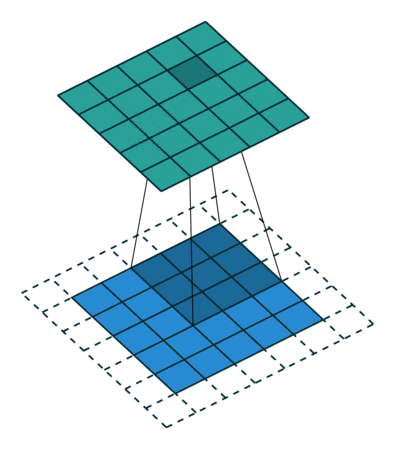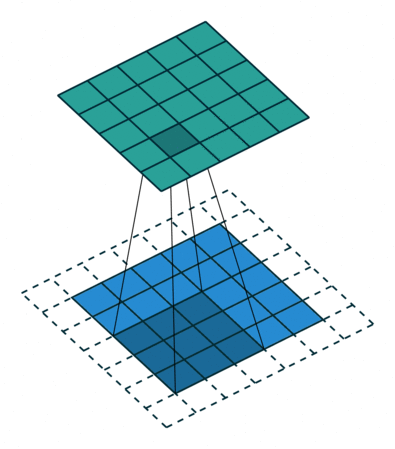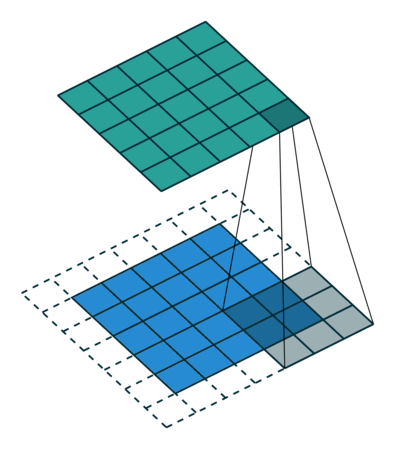
正卷积 Convolution
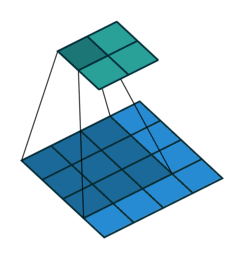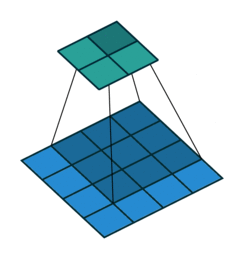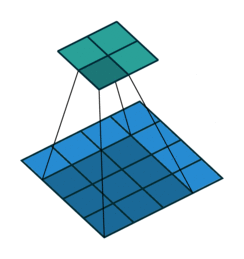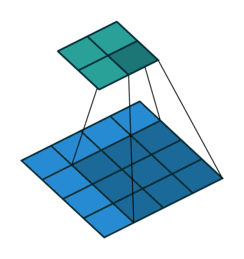 |
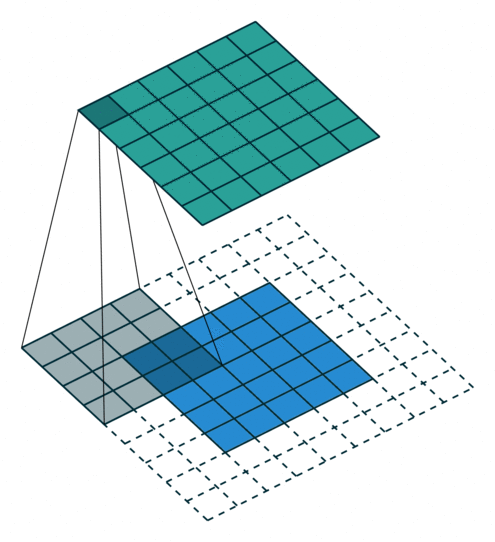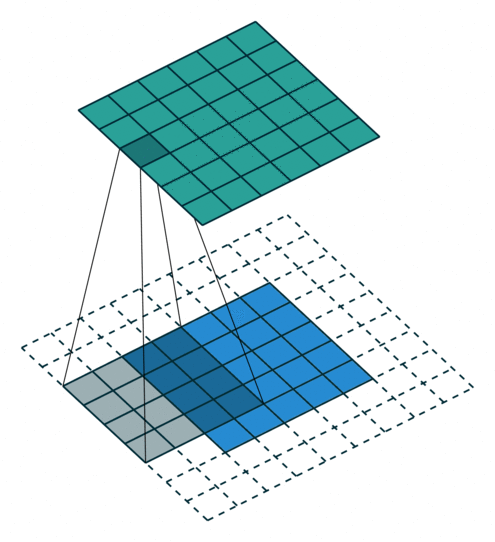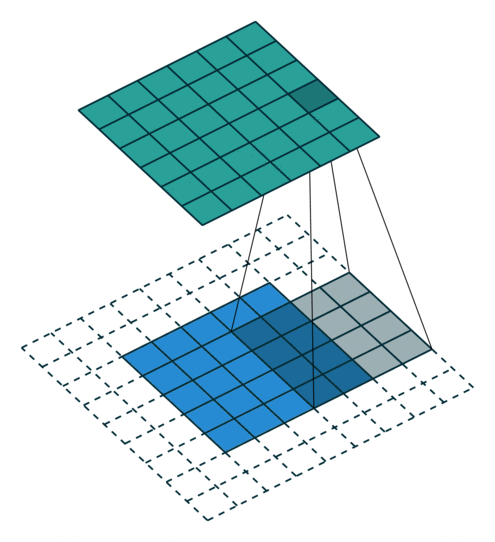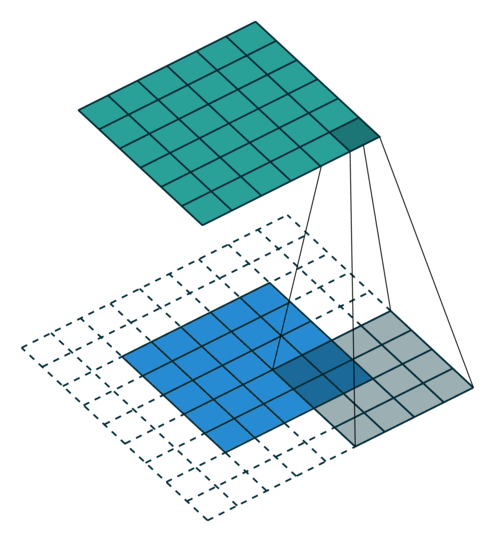 |
 |
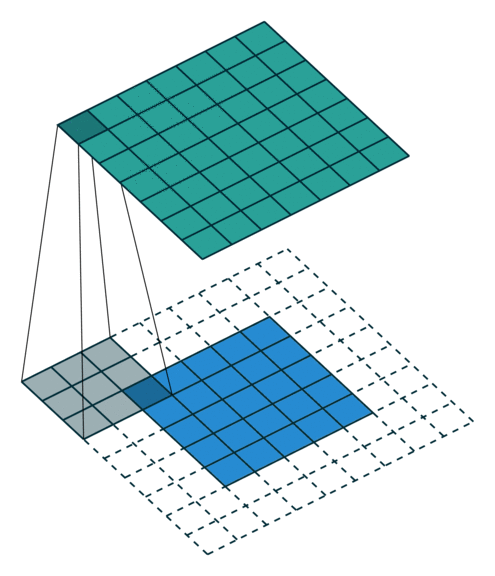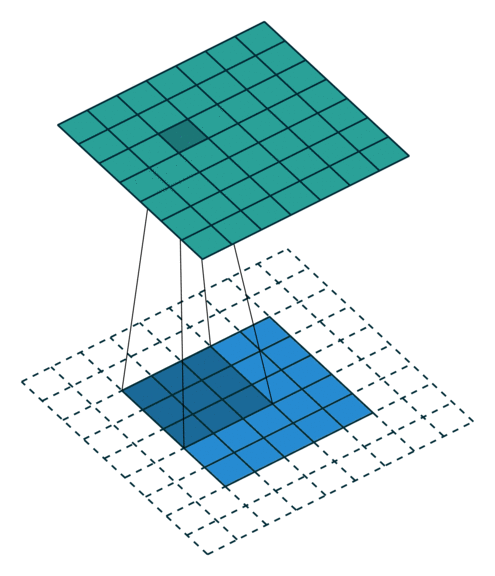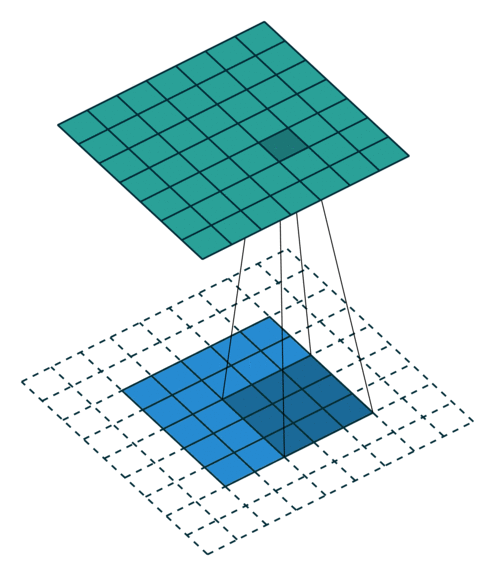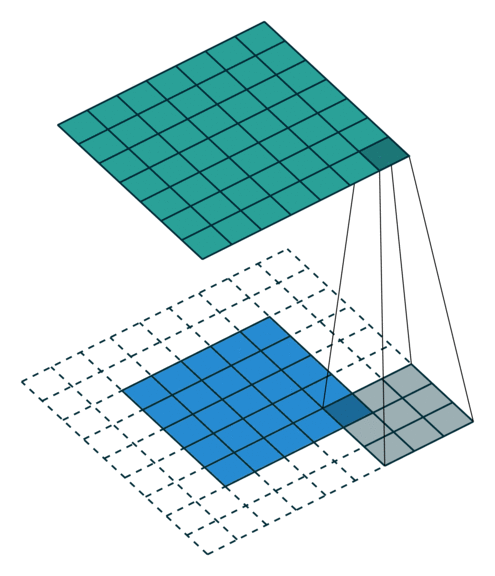 |
| No padding, no strides | Arbitrary padding, no strides | Half padding, no strides | Full padding, no strides |
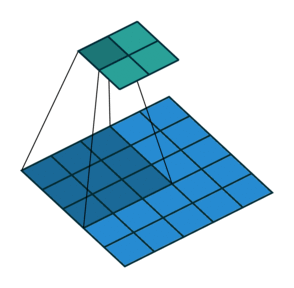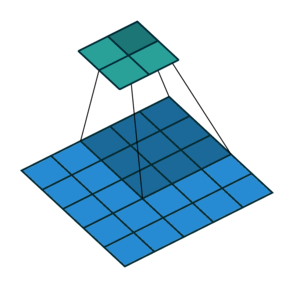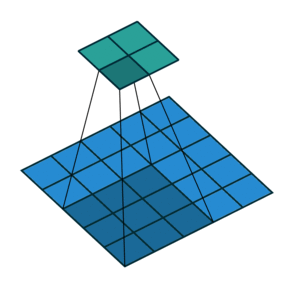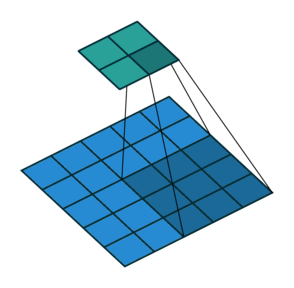 |
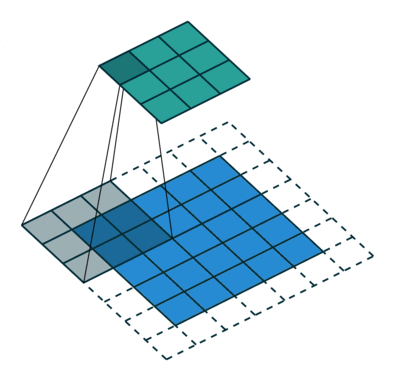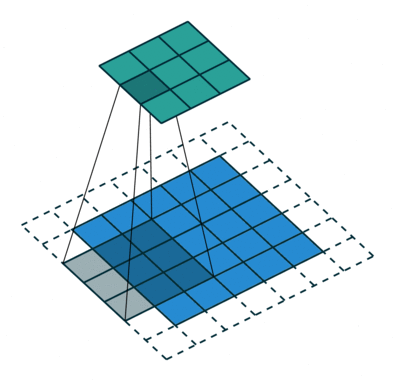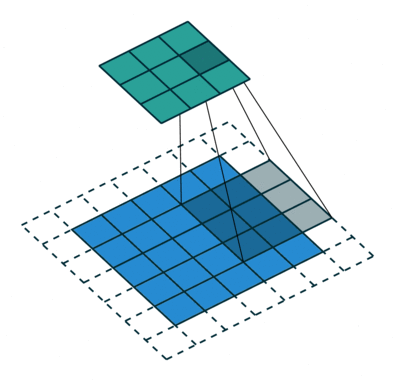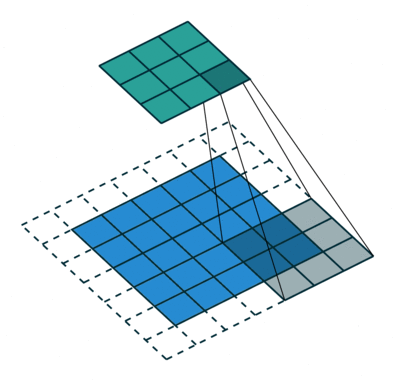 |
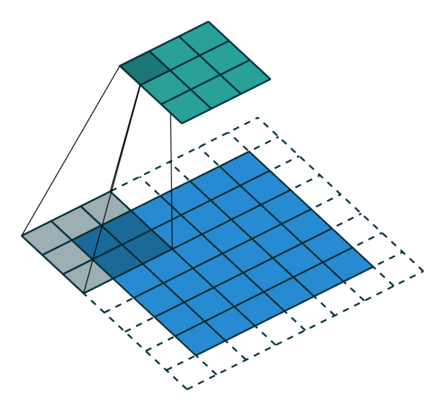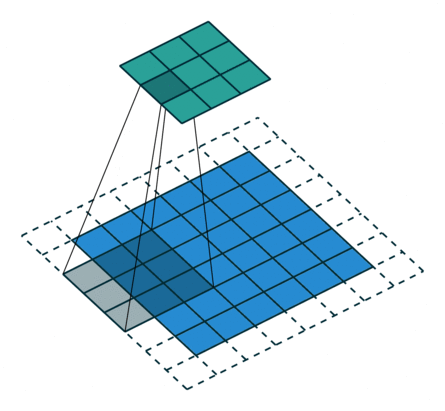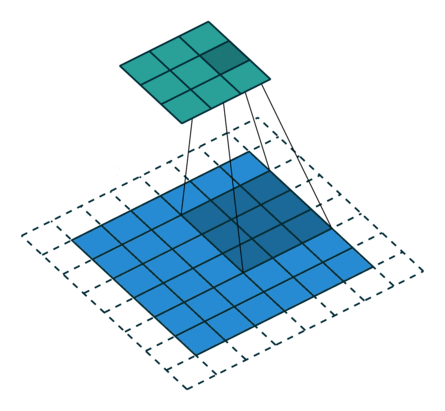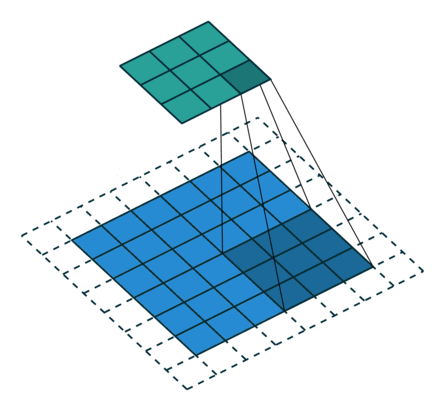 |
|
| No padding, strides | Padding, strides | Padding, strides (odd) |
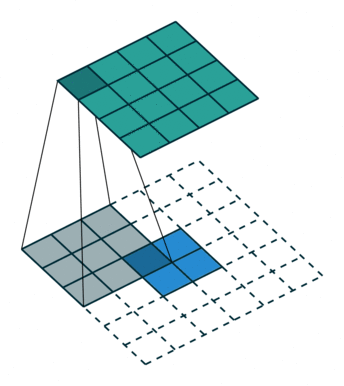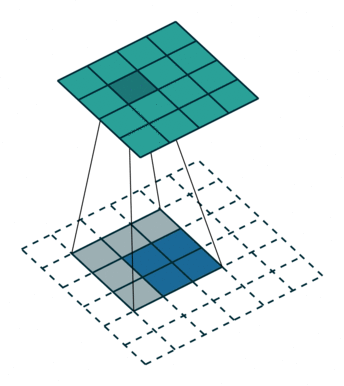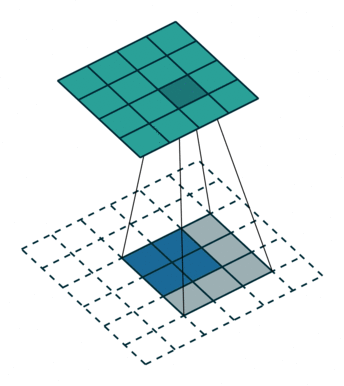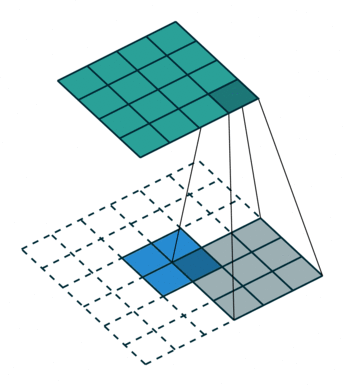
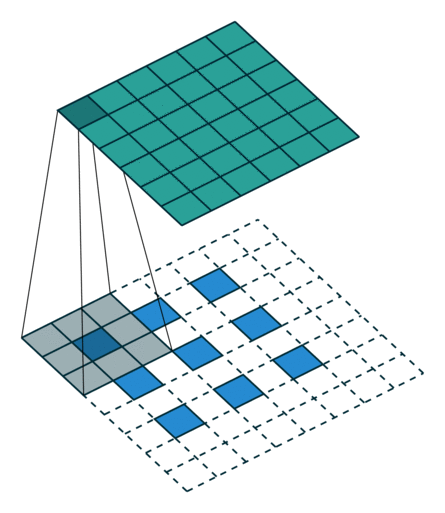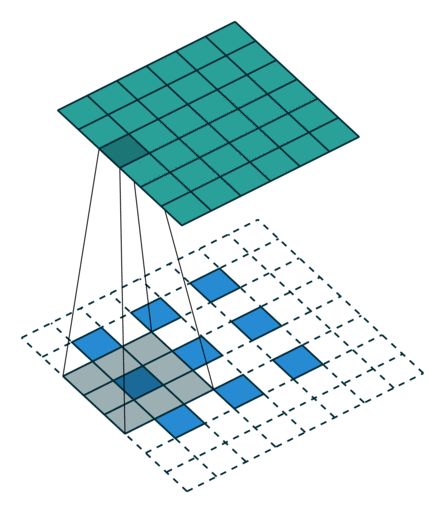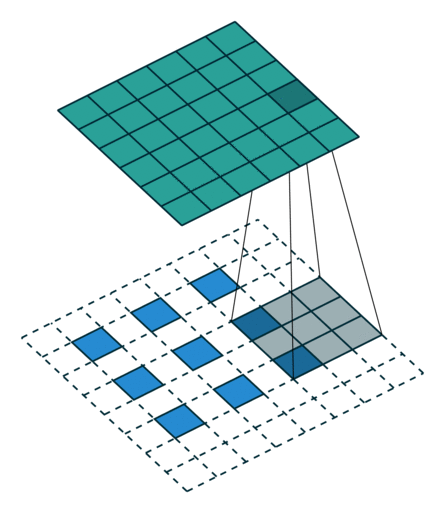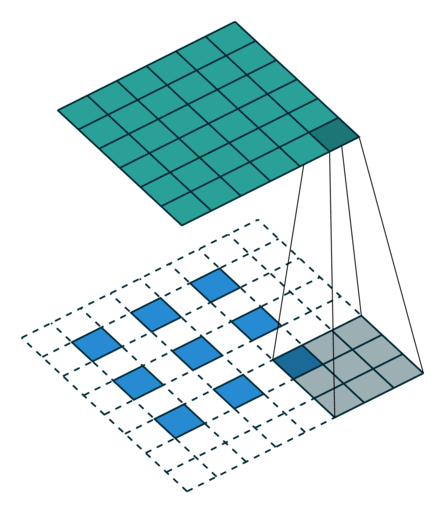
转置卷积 Transposed Convolution
 |
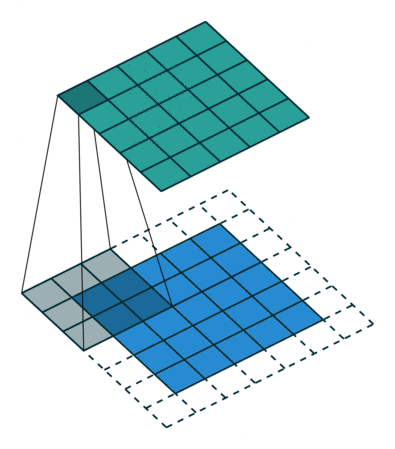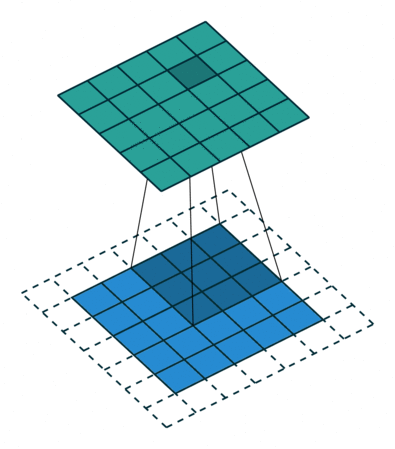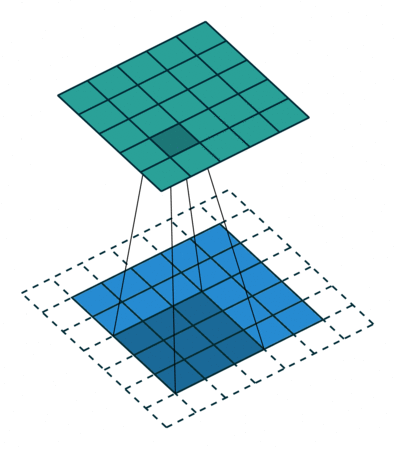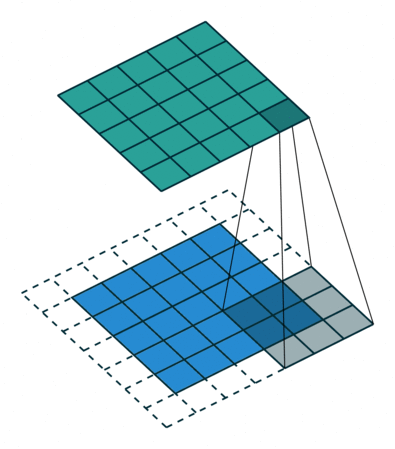 |
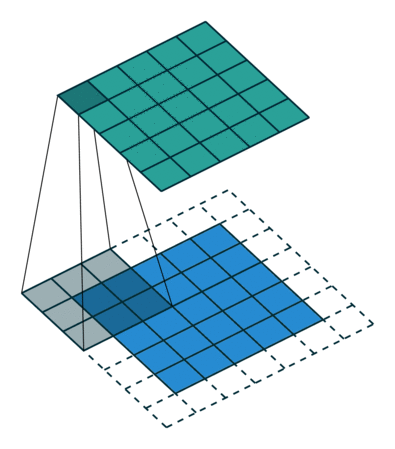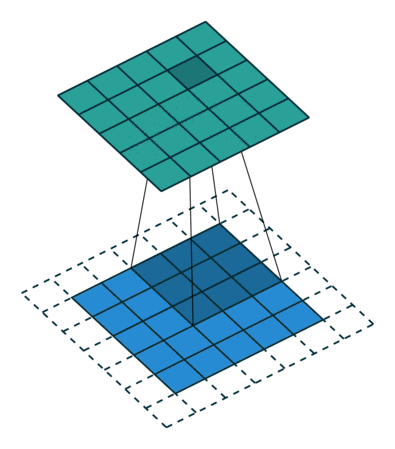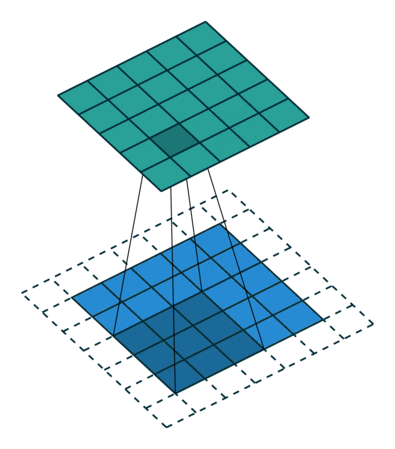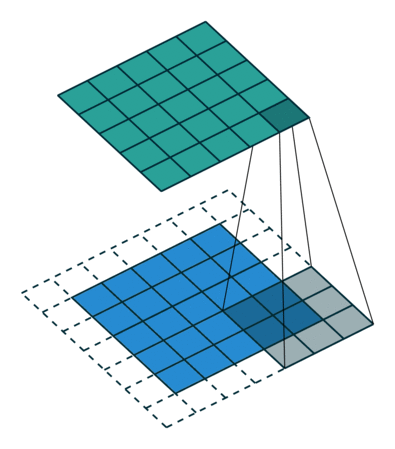 |
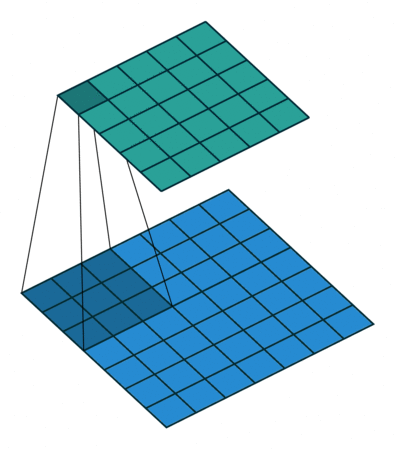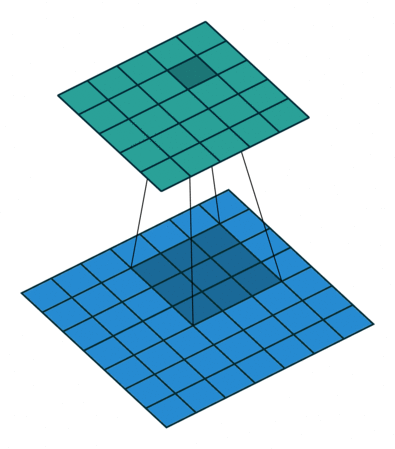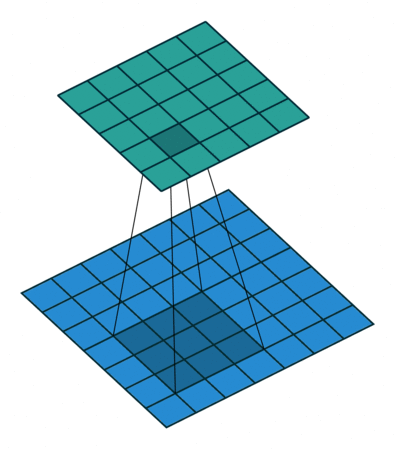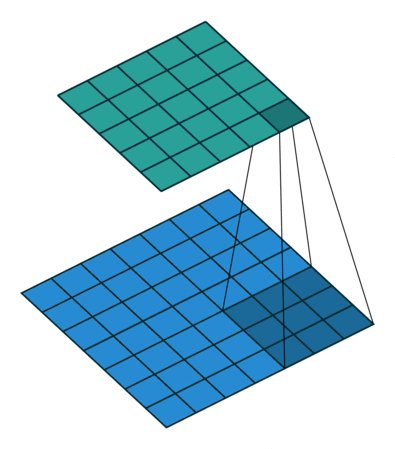 |
| No padding, no strides, transposed | Arbitrary padding, no strides, transposed | Half padding, no strides, transposed | Full padding, no strides, transposed |
 |
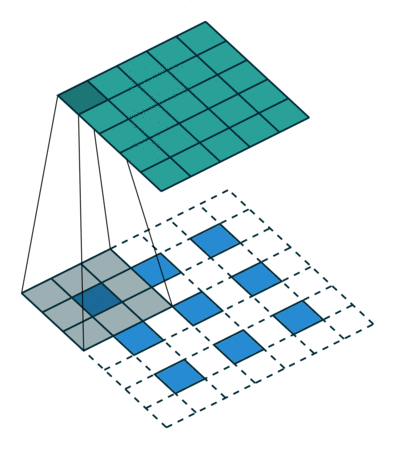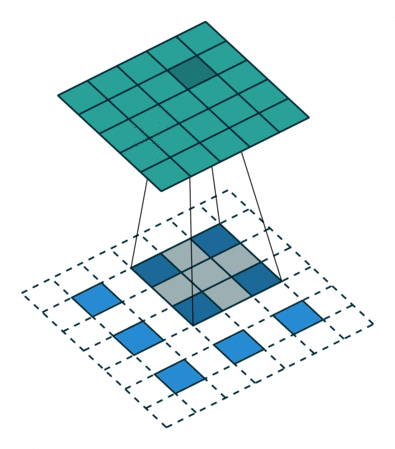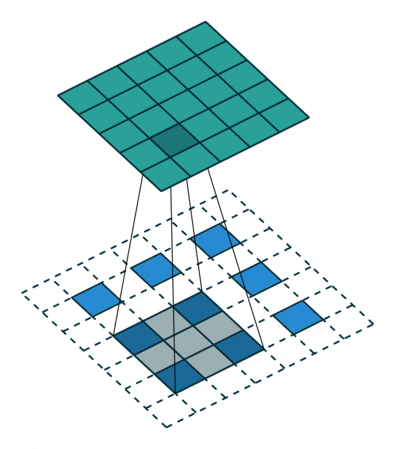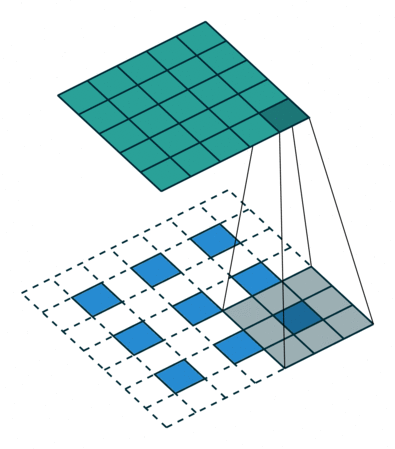 |
 |
|
| No padding, strides, transposed | Padding, strides, transposed | Padding, strides, transposed (odd) |
4 多输入输出通道channls
意义
多个输出out通道可以识别特定的模式,Eg:RGB图片三通道可以按照颜色分别识别
多个输入in通道可以识别并组合输入中的模式,Eg:在识别猫的图片时,分别识别出猫的脚和身体,然后组合
实现
多输入in:在每个通道各自卷积后加权求和(降维)为一个通道
多输出out:使用多个卷积核,每个卷积核生成一个输出通道
5 1x1的卷积层
不识别空间模式,只是融合不同通道的信息,对不同的通道进行加权求和
Eg:语音分离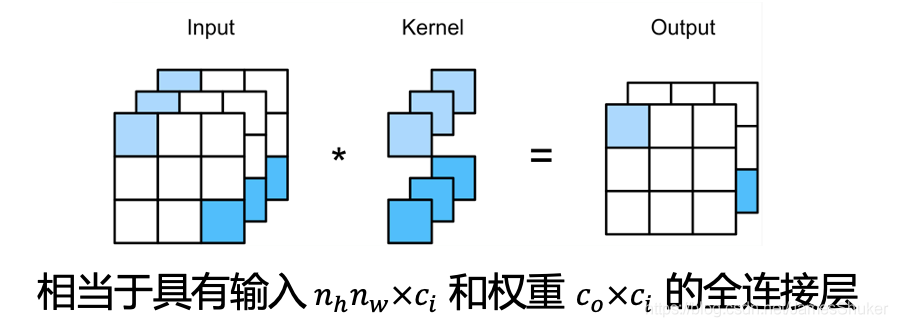
将input拉成一维的向量就变成全连接层
五、ConvTranspoes 转置卷积
增大输入的高宽,一般用于恢复形状,但输出的信息比较抽象,不能被人直接分辨,也用于上采样。
输入中的每一个值与卷积核的每一个值做乘法,把重合的部分相加。
padding是去掉输出的外层。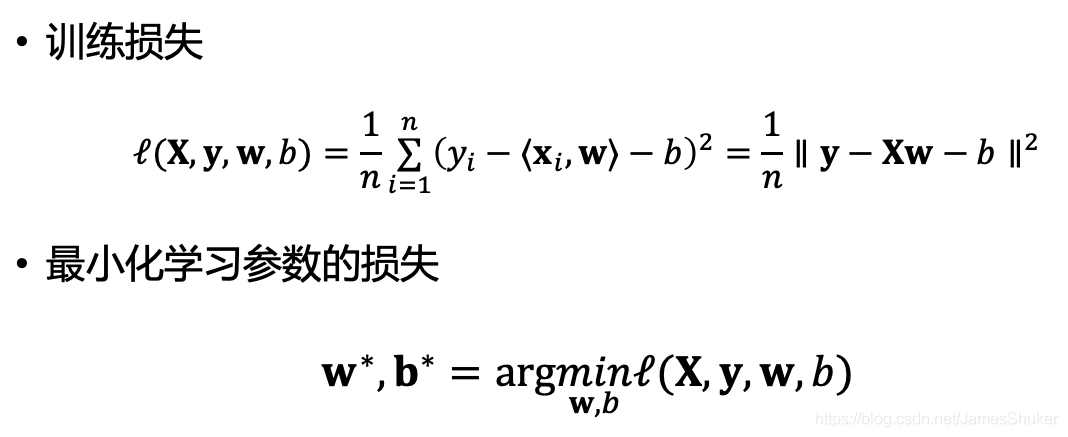
六、池化层(汇聚层) Pooling
卷积层做边缘检测时,对边缘太敏感,检测时往往会不准确
最大池化:在滑动窗口时,返回窗口中的最大值
平均池化:返回窗口中各元素的均值
特点
超参数有窗口大小、填充和步幅
没有可学习的参数
输出通道数=输入通道数
在每个输入通道都用池化层来分别获得输出,不进行多通道融合
torch实现
2x3大小的窗口
pool2d = nn.MaxPool2d((2, 3), padding=(1, 1), stride=(2, 3))
pool2d(X)