基础算法

排序

快速排序 - 分治

分治：不断把数据分成两部分，一半小于另一半

1. 确定分界（4种方法）：取q[l], q[(l + r) / 2], q[r], 随机点

2. 调整区间：小于分界点的在左区间，其余在右区间

   ​ 使用两个数组作为左右区间

   ​ 使用两个指针（i = l - 1，j = r + 1），如果a[i]>x,a[i]<x，交换a[i] a[j]

3. 递归：给左右排序

void quick_sort(int q[], int l, int r) {
    if (l >= r) 
      return;

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j) {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j); quick_sort(q, j + 1, r);
}

归并排序 - 分治（稳定）

合并：两个有序数组

双指针：比较两个数组里待合并的数，将较小的放入新数组

1. 确定分界点 mid = (l + r) / 2 数组的中心
2. 递归
3. 归并两个有序数组（用双指针合并）

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;

    int mid = l + r >> 1; // 用mid将原数组一分为二
    // 先递归到底
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) 
        // 双指针i和j分别对mid左右的两个数组遍历
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    // 将剩余的部分加入数组
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

二分

有单调性 一定可以 二分

求范围，让答案在收缩的区间里

向左收缩和向右收缩mid的取值不同

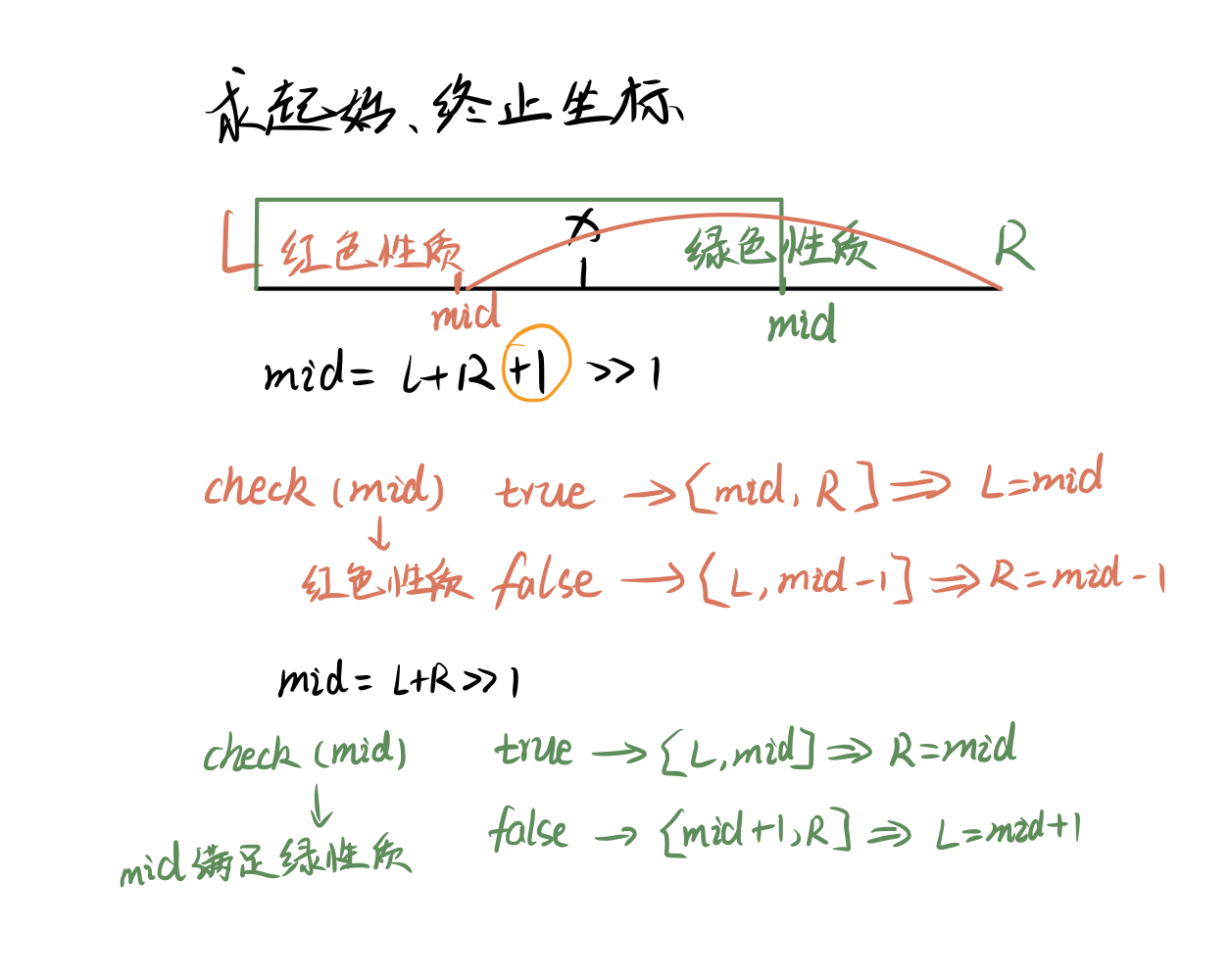
// 整数二分
bool check(int x) {} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：向左收缩
int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    } // 结束时l和r相等
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：向右收缩
int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;//防止死循环 多加1
        if (check(mid)) l = mid; // arr[mid]=x 时需要取边界
        else r = mid - 1;
    }
    return l;
}

对于浮点数 将while里停止的条件改为 r - l > 1e-6

while控制的精度最好小于输出保留位数两位，防止精度不够

Eg：输出小数点后四位，这里控制为1e-6

// 实数二分
bool check(double x) {} // 检查x是否满足某种性质

double bsearch_3(double l, double r) {
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

高精度

用数组存大整数，低地址存低位（小端），0存个位

加

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B) {
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ ) {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

减

A < B => -(B - A)

// C = A - B, 满足A >= B, A >= 0, B >= 0
bool cmp(vector<int> &A, vector<int> &B) {
    if (A.size() != B.size()) return A.size() > B.size();
    for (int i = A.size()-1; i >= 0; i--) 
        if (A[i] != B[i]) return A[i] > B[i];
    return true; // 
}
vector<int> sub(vector<int> &A, vector<int> &B) { //引用 节省时间
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ ) {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
          // 只防止负数 不会改变结果 
        //（1+10）%10 = 1 （10+10）%10 = 0
        if (t < 0) t = 1;
        else t = 0;
    }
        // 去除多个 0
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
// 主函数
if (cmp(A, B)) C = sub(A, B);
else {
    C = sub(B, A);
    cout<<'-';
}

乘

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b) {
    vector<int> C;

    for (int i = 0, t = 0; i < A.size() || t; i ++ ) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

除

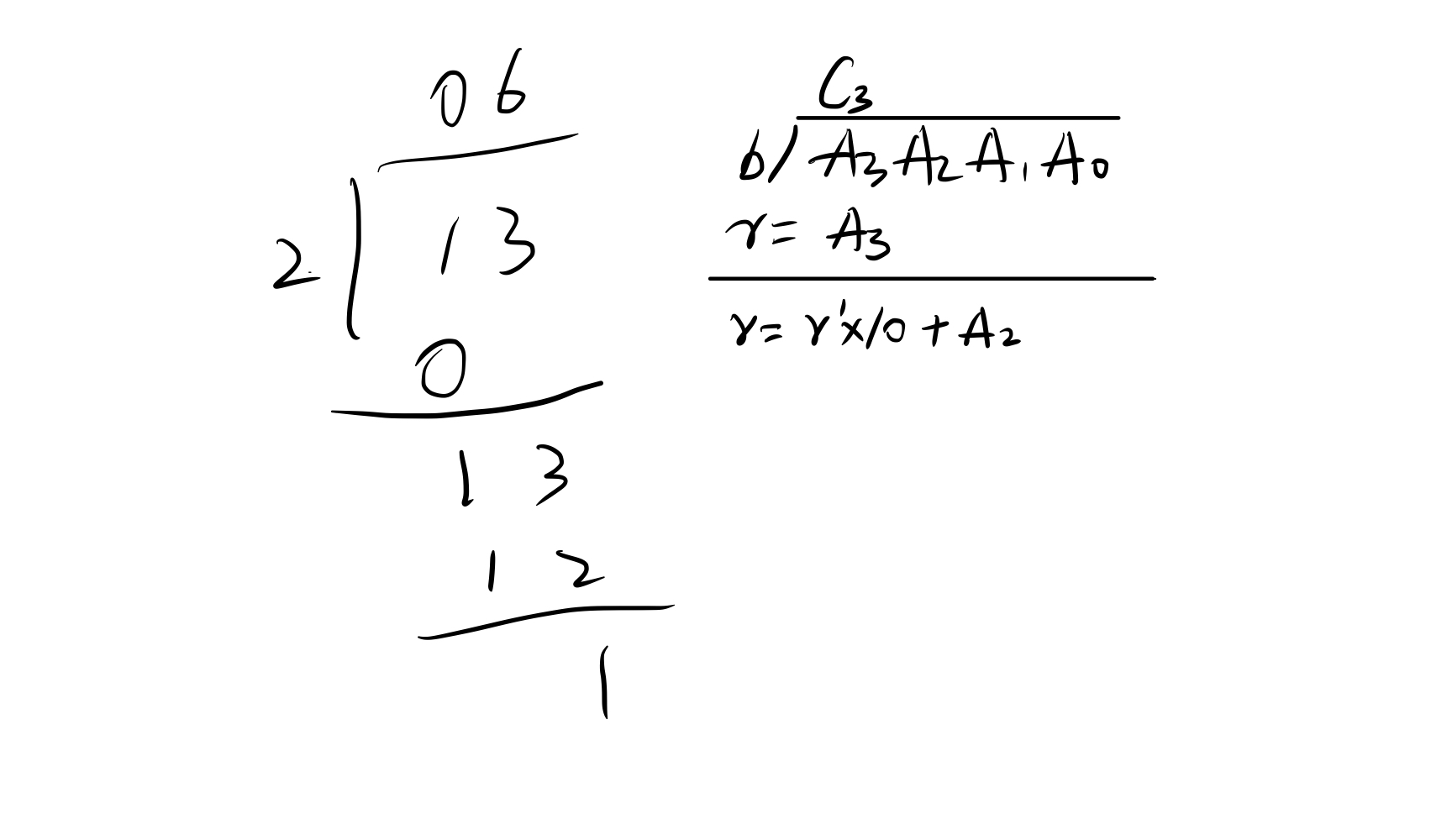
// A / b = C ... r, A >= 0, b > 0
// 引用直接修改原来的r
vector<int> div(vector<int> &A, int b, int &r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- ) {
        r = r * 10 + A[i]; // 借位
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

前缀和

应用：计算前缀和

存前缀和的下标从1开始，将数组下标为0的值设为0

一维

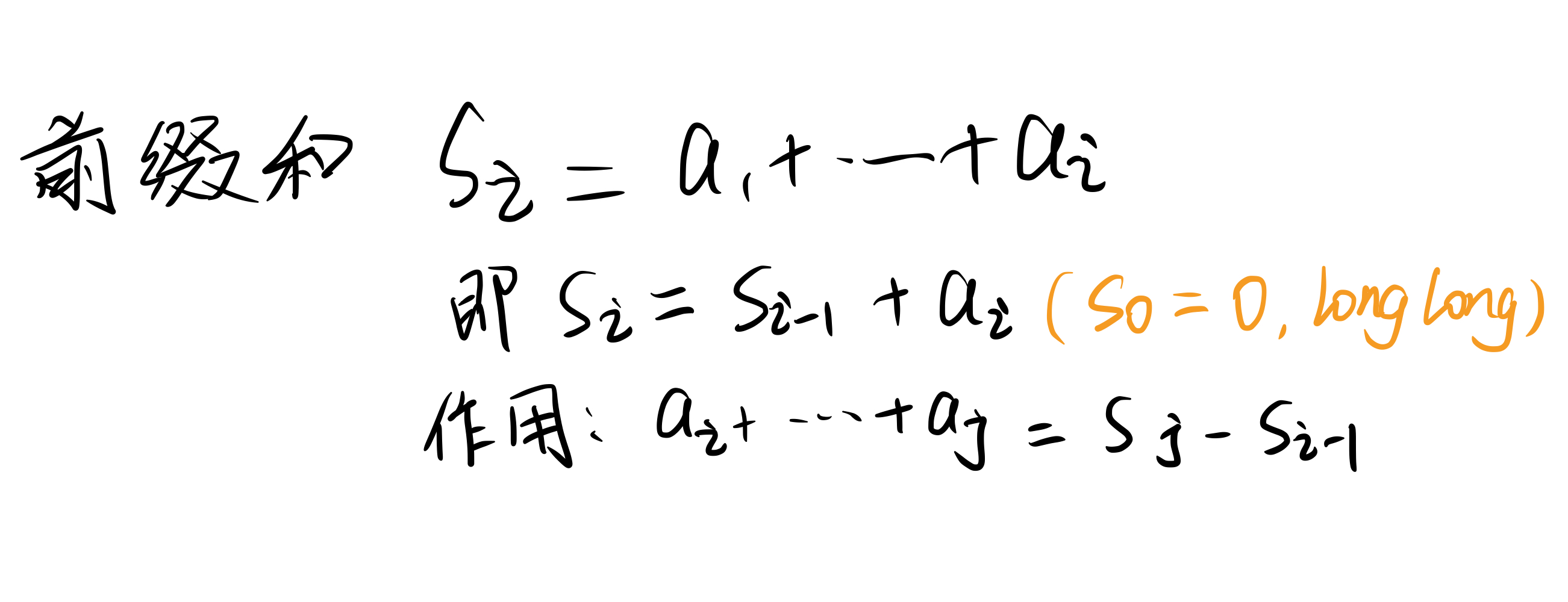
二维

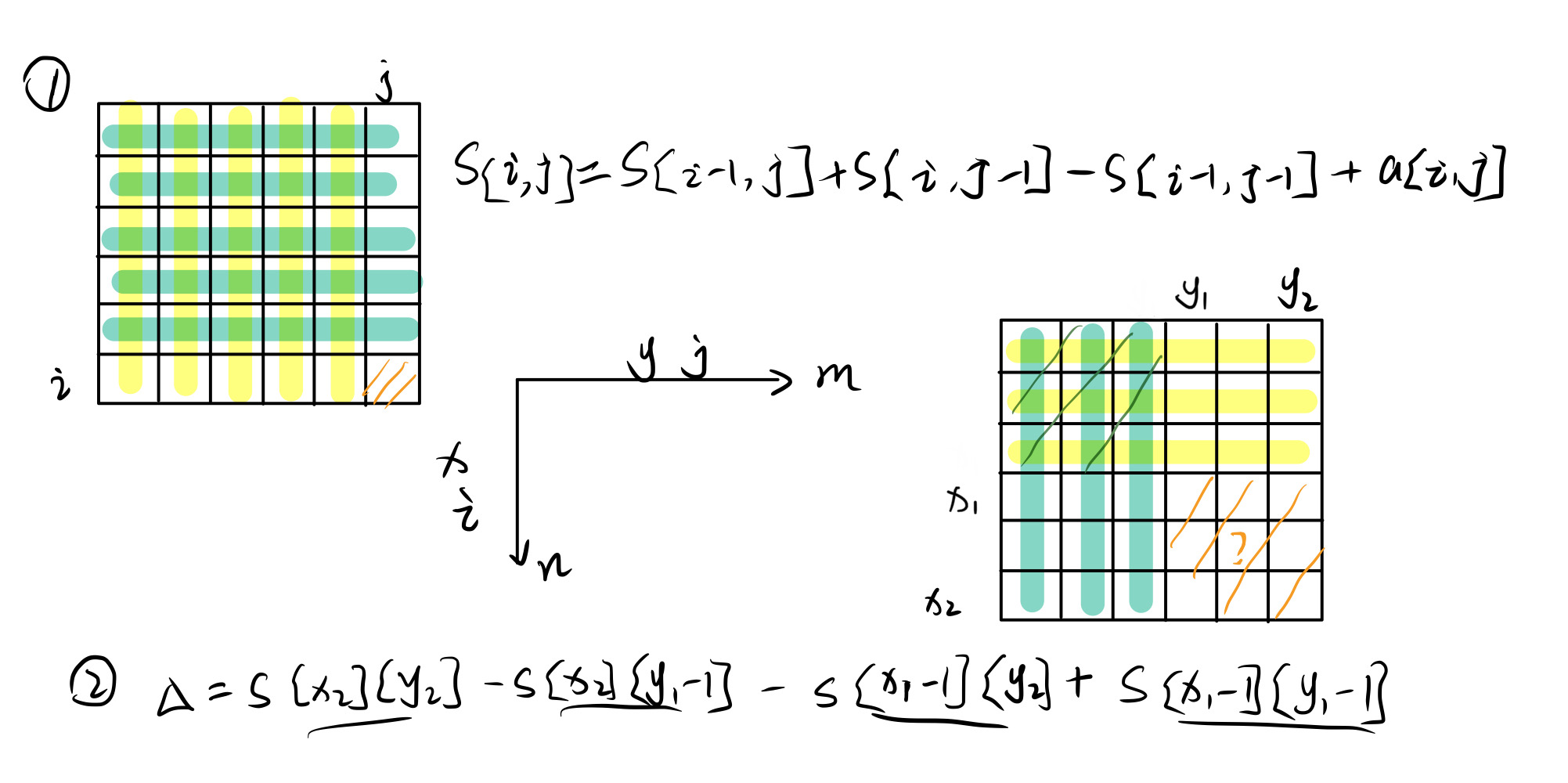
// 一维
s[i] = s[i-1] + a[i];
s[j] - s[i-1];

// 二维
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j];
sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];

差分

应用：在[ l , r ]之间的每个数加上 c

前缀和的逆运算

一维

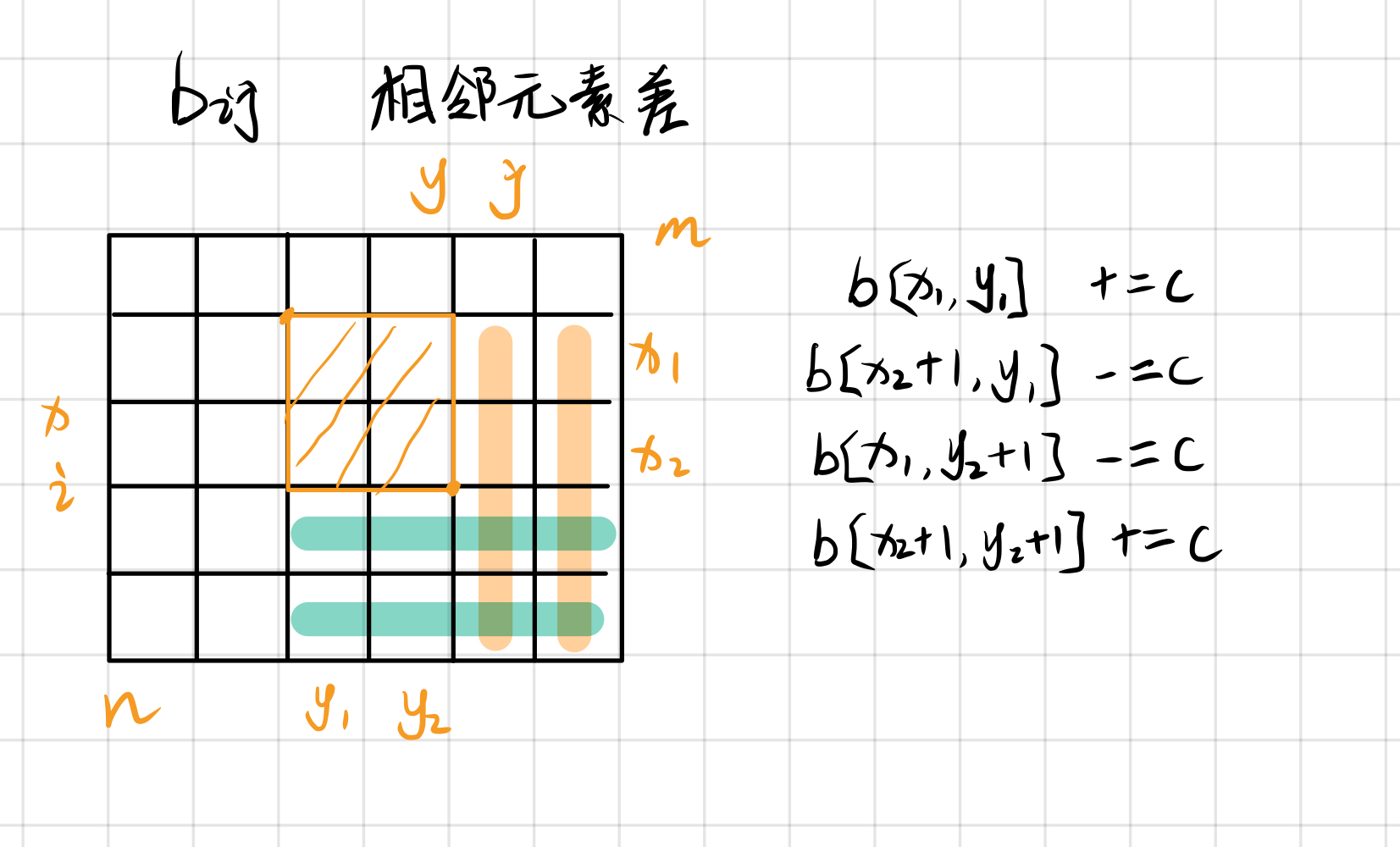
二维

// 一维
// a存b的前缀和
b[i] = a[i]-a[i-1]

void insert(int l, int r,int c) {
  b[l] += c;
  b[r+1] -= c;
}
// 求前缀和 得到操作后的a数组
b[i] += b[i-1];

// 二维
void insert(int x1,int y1,int x2,int y2,int c) {
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}
// 求前缀和 把b还原成加了c之后的a
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];

双指针

核心：将两个指针 n^2 优化到 n ， 没思路可以先写一个 n^2 找规律

两个序列：合并；归并排序的归并、快速排序的划分；KMP

一个序列：确定区间的开头结尾，如：滑动窗口；判断环

for (i = 0, j = 0; i < n; i++) {
    while(j < i && check(i, j)) j++;
}

位运算

n>>k&1：n（二进制）的第k位（从第0位开始）

1<<n：2的n次方

lowbit(x) { return x&-x;}：x&(~x+1)，即返回x的最后一位1，可以计算1的个数

异或

不进位加法，相同为0，不同为1

运算	功能
0^x = x	0异或还是原数
1^1010 = 1011	1异或末尾取反
x^x = 0	异或自己得0
a^b == 0	判断a和b是否相等

交换a和b：a = a ^ b, b = b ^ a, a = a ^ b

交换律： a ^ b = b ^a, a ^ b ^ a = b 可以用于找奇数个数的数

离散化

离散化：稀疏数组中，10^5个数，值域为 0 ~ 10^9，将值域映射到 0 ~ n

难点：可能存在重复元素，并能及时得到离散化后的值

应用：稀疏数组即数组下标很大，但数组中很多值是空的

// 用vector模拟set，可以用下标访问
vector<int> vec;
sort(vec.begin(), vec.end()); // 排序
vec.erase(unique(vec.begin(), vec.end()), vec.end()); // 去重
// 用二分找第一个大于等于x的，相当于lower_bound()
int find(int x) { 
    int l = 0, r = vec.size()-1;
    while (l < r) {
        int mid = l+r>>1;
        if (vec[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r+1; // 从1开始映射
}

数据结构

链表

单链表

/*
* head 头结点下标 存值
* e 存val
* ne 存next
* idx 表示e中当前位置
*/
int head, e[N], ne[N], idx;
// 头插
void add_to_head(int x) {
    e[idx] = x;
    ne[idx] = head;
    head = idx;
    idx ++;
}
// 下标为k的后面插x
void add(int k, int x) { 
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx ++;
}
// 删k后的点 (-1后的点为0)
void remove(int k) {
    if (k == -1) head = ne[head];
    ne[k] = ne[ne[k]];
}
void init() {
    head = -1;
    idx = 0;
}

邻接表

int head[N];

双链表

优化某些问题

int head, tail;
int e[N], l[N], r[N], idx;
void init() {
    head = -1; 
    tail = -1;
    idx = 0;
}
// 在k右边插入 
// 在k左边插入 add(l[k], x);
void add(int k, int x) {
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    l[r[k]] = idx;
    r[k] = idx;
    idx ++;
}
void remove(int k) {
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

栈

单调栈

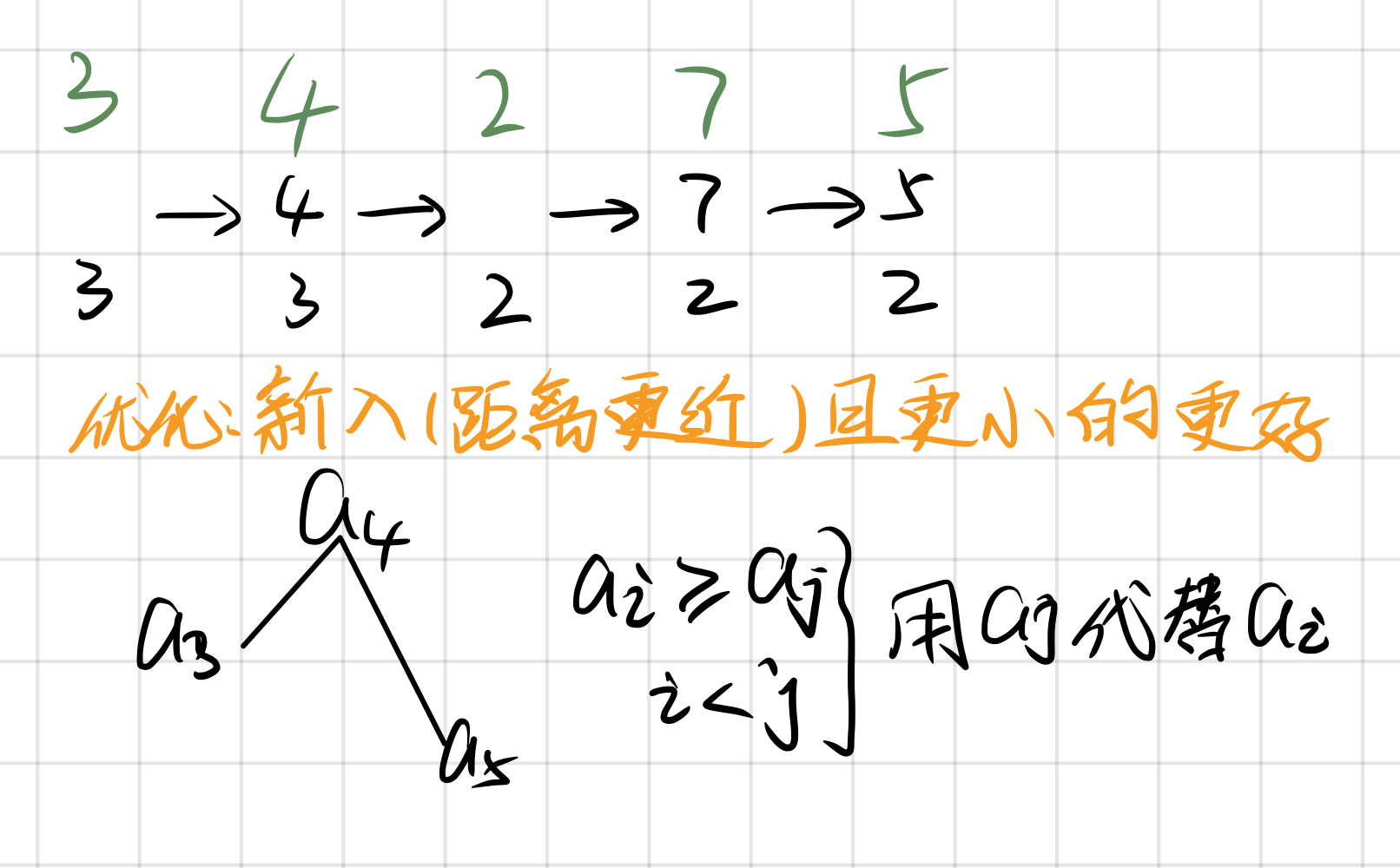
应用：找每个数左边第一个比它小/大的数、视野总和、柱状图中最大矩形

有序栈：如果栈为空或入栈元素值小于栈顶元素值，则入栈；否则，如果入栈则会破坏栈的单调性，则需要把比入栈元素小的元素全部出栈。

思想：先考虑暴力，然后优化

// STL
for (int i = 0; i < n; i ++ ) {
    cin>>x;
    while (!stk.empty() && stk.top() >= x) stk.pop();
    if (!stk.empty()) cout<<stk.top();
    else cout<<-1;
    cout<<' ';
    stk.push(x);
}
// 数组
for (int i = 0; i < n; i ++ ) {
  cin>>x;
  while (tt && stk[tt] >= x) tt --;
  if (tt) cout<<stk[tt];
  else cout<<-1;
  cout<<' ';
  stk[++tt] = x;
}

队列

单调队列（滑动窗口）

思路：先暴力 再优化，根据单调性，去除不必要的数据和遍历

// 数组模拟队列
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ ) {
  while (hh <= tt && q[hh] < i-k+1) hh++;
  while (hh <= tt && a[q[tt]] >= a[i]) tt--;

    q[++tt] = i;
    if (i >= k-1) cout<<a[q[hh]]<<' ';
}
// 双端队列
deque<int> que;
for (int i = 0; i < n; i ++ ) {
  while (!que.empty() && que.front() < i-k+1) que.pop_front(); // 超出窗口大小出队
  // 次新的不如新的小 丢弃
  while (!que.empty() && a[i] <= a[que.back()]) que.pop_back();

  que.push_back(i);
  if (i >= k-1) cout<<a[que.front()]<<' ';
}
// 优先队列
priority_queue<PII, vector<PII>, greater<PII>> que1;
for (int i = 0; i < n; i ++ ) {
    while (!que1.empty() && que1.top().y < i-k+1) que1.pop();

  que1.push({a[i], i});
  if (que1.size() > k-1) cout<<que1.top().x<<' ';
}

KMP

应用：找子串

// 求next
for (int i = 2, j = 0; i <= n; i ++ ) {
    while (j && p[i] != p[j+1]) j = ne[j];
  if (p[i] == p[j+1]) j++;
  ne[i] = j;
}

for (int i = 1, j = 0; i <= m; i ++ ) {
    while (j && s[i] != p[j+1]) { // 不能匹配或j无处可退
      j = ne[j];
  }
  if (s[i] == p[j+1]) j++;
  if (j == n) {
        // 匹配成功
    cout<<i-n<<' ';
    j = ne[j]; // 
  }
}

Trie树

高效存储查找字符串集合

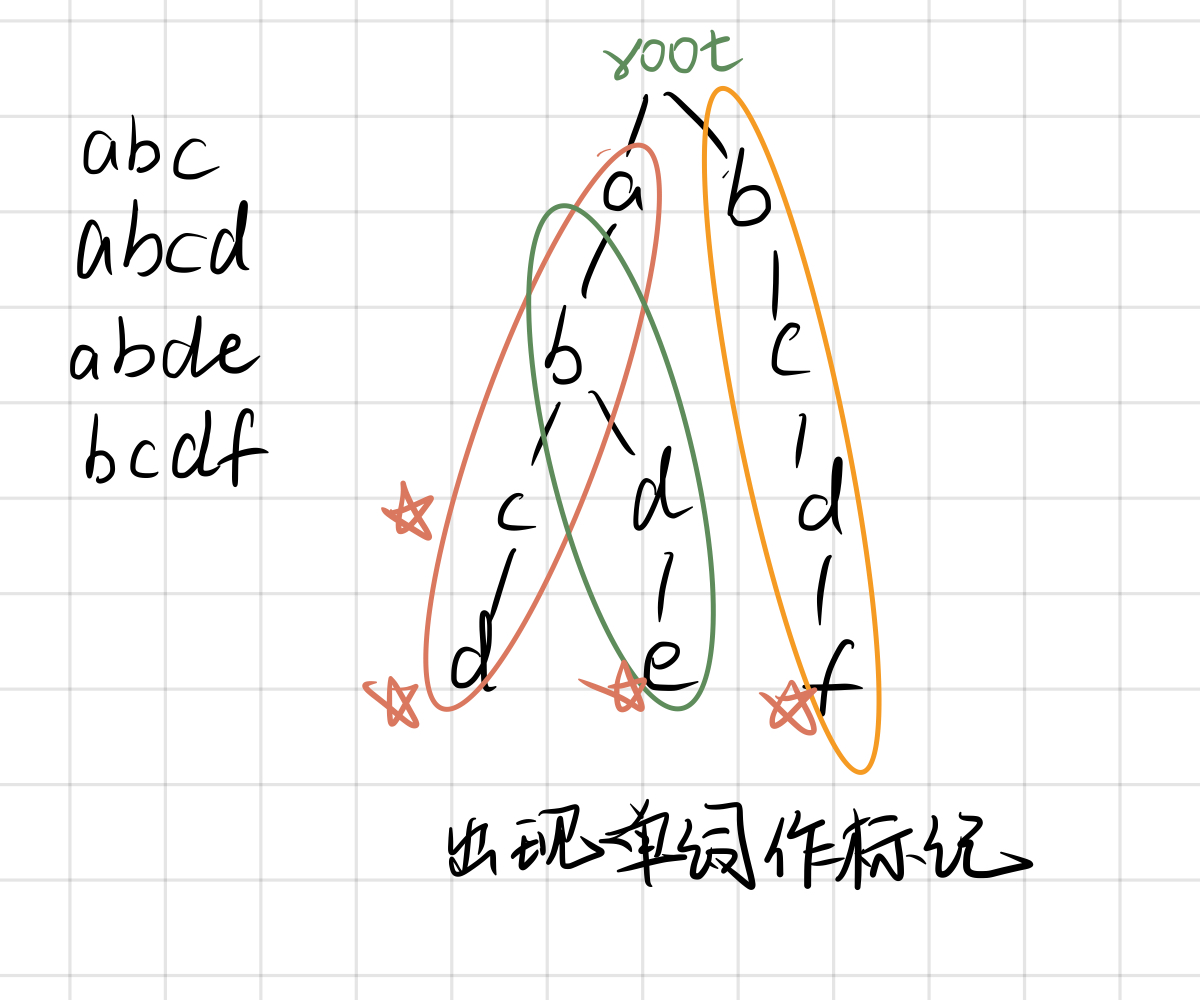
// son每个结点的子节点
// cnt以当前点结尾的单词的数量
// 下标为0的点 空节点或者根节点
int son[N][26], cnt[N], idx; 
void insert(char str[]) {
    int p = 0;
    for (int i = 0; str[i] ;i++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx; // 不存在字母u
        p = son[p][u];
    }
    cnt[p] ++;
}
int query(char str[]) { // 返回string出现的次数
    int p = 0;
    for (int i = 0; str[i] ;i++ ) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

并查集 Union Find Set

合并两个集合、询问两个元素是否在一个集合中

基本：树根（代表元素）的编号是整个树的编号

路径压缩：所有孩子都直接指向根节点

按秩合并：将简单的树合并在复杂的树下（计算深度）

朴素并查集

int p[N]; //储存每个点的祖宗节点

int find(int x) { //返回x的祖宗节点 + 递归保证 路径压缩
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

for (int i = 1; i <= n; i ++ ) p[i] = i; //初始化

p[find(a)] = find(b); //合并a,b两个集合

维护size数组的并查集

int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

// 返回x的祖宗节点
int find(int x){
  if (p[x] != x) p[x] = find(p[x]);
  return p[x];
}
// 初始化，假定节点编号是1~n    
for (int i = 1; i <= n; i ++ ){
  p[i] = i;    
  size[i] = 1;
}
// 合并a和b所在的两个集合：先把size求和    
size[find(b)] += size[find(a)];
p[find(a)] = find(b);

维护到祖宗节点距离的并查集

int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

// 返回x的祖宗节点
int find(int x){
    if (p[x] != x){
        int u = find(p[x]);
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ){
    p[i] = i;
    d[i] = 0;
}

// 合并a和b所在的两个集合：
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

堆

完全二叉树

根结点小于等于左右子结点

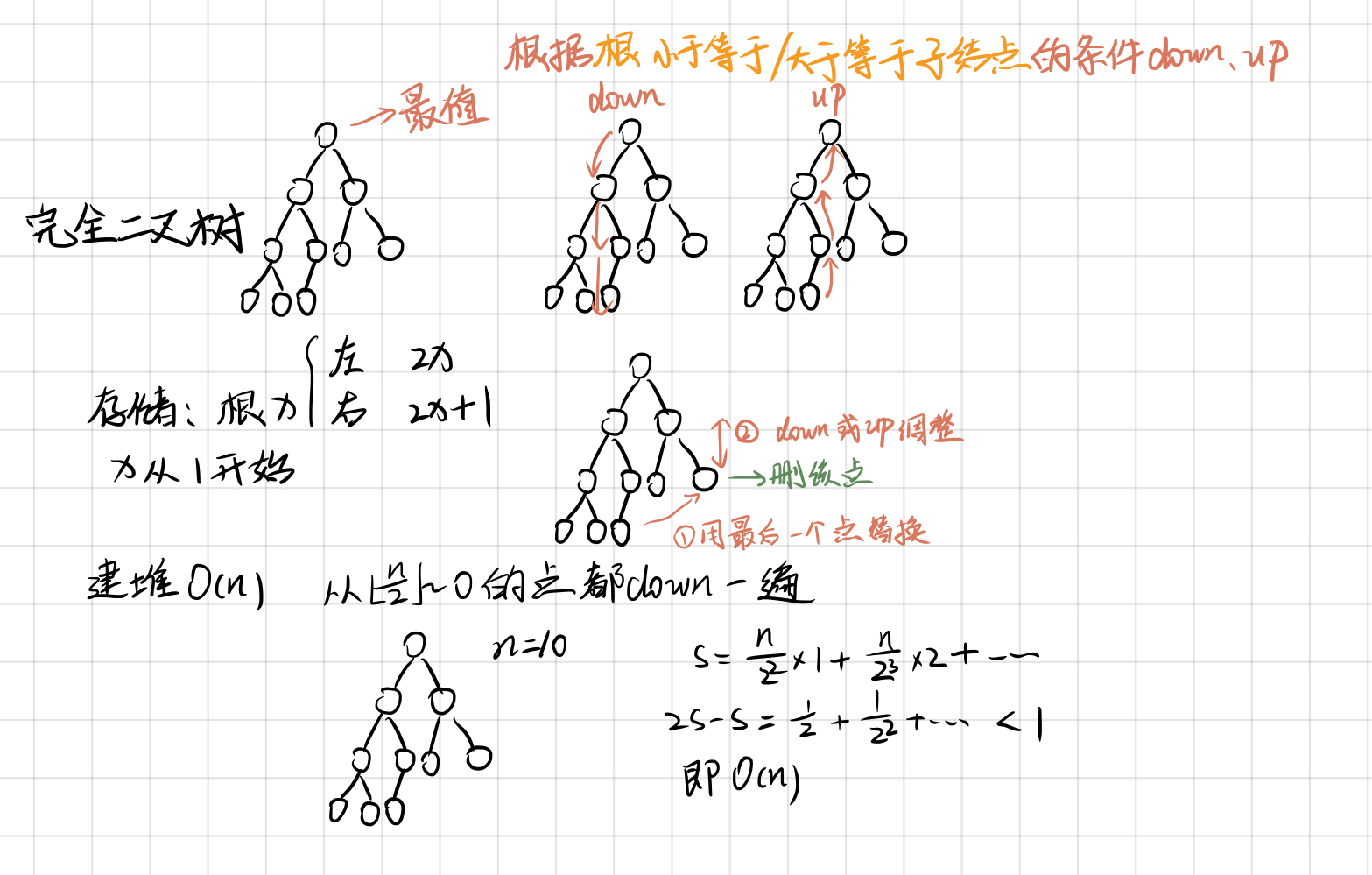
int h[N]; // 用完全二叉树存堆
// 从根往下调整
void down(int u) {
  int t = u;
  if (u*2 <= size && h[u*2] < h[t]) t = u*2;
  if (u*2+1 <= size && h[u*2+1] < h[t]) t = u*@+1;
  if (u != t) {
    swap(h[u], h[t]);
    down(t);
  }
}
void up(); // 向上调整
// 插入
heap[++size] = x; up(size);
// 求最值（堆顶）
head[1]
// 删除最值
heap[1] = heap[size]; size --; down(1);
// 删除任意元素（用最后一个代替原值并执行down或up，这里都写但实际不会都执行下去）
heap[k] = heap[size]; size --; down(k); up(k);
// 修改任意值
heap[k] = x; down(k); up(k);

搜索与图论

DFS

深搜

BFS

广搜

八皇后

拓扑排序

关键：广搜、入度

bool topsort() {
    queue<int> que;
    for (int i = 1; i <= n; i++) // 初始化 将入度为0的点入队
        if (d[i] == 0) que.push(i);

    while(!que.empty()) {
        int tmp = que.front();
        ans.push_back(tmp);
        que.pop();

        for (auto e : edge[tmp]) {
            d[e] --;
            if (d[e] == 0) que.push(e);
        }
    }
    return ans.size() == n; // 全进入ans则存在拓扑
}

最短路径

n为点数，m为边数

分类

朴素Dijkstra

稠密图用邻接矩阵

重边保留短边，忽略自环

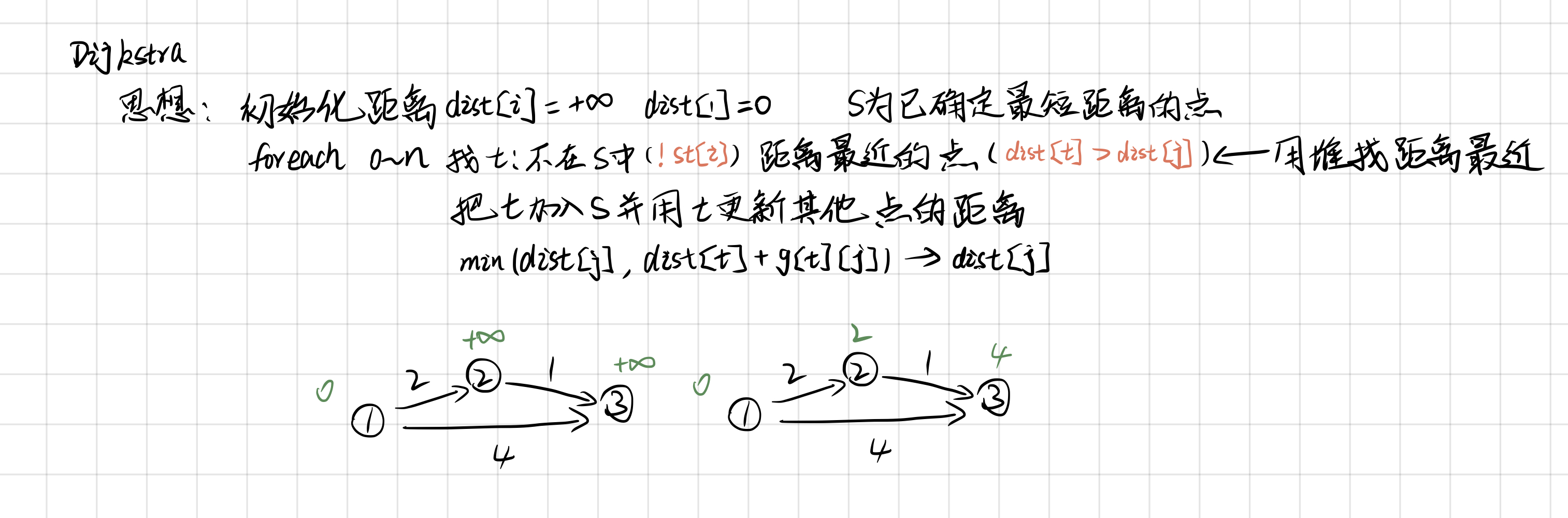
int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra() {
    memset(dist, 0x3f, sizeof dist); //初始化 dist 为无穷
    dist[1] = 0;
    for (int i = 0; i < n - 1; i++) {
        int t = -1;     // 在还未确定最短路的点中，找距离最小的点
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        // 用t更新其他点的距离
        for (int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        st[t] = true;
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

堆优化Dijkstra

稀疏图用邻接表

const int N = 510; // 太大会爆vector
typedef pair<int,int> PII;
int n, m, dist[N], weight[N][N];
memset(weight, 0x3f, sizeof weight);
vector<int> g[N];
bool st[N]; 
int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    priority_queue<PII,vector<PII>,greater<>> heap; // 小顶堆
    heap.push({0,1}); // first->距离 second->点 用距离排序
    while (!heap.empty()) {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;
        if (st[ver]) continue;
        st[ver] = true
        for (auto vec : g[ver]) {
            if (dist[vec] > distance + weight[ver][vec]) {
                dist[vec] = distance + weight[ver][vec];
                heap.push({dist[vec], vec});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

Bellman-Ford

数学

数论

质（素）数

大于等于2的整数中，只包含1和本身这两个约数

质数判断一试除法：

bool is_prime(int n) {
    if (n < 2) return false;
    for (int i = 2; i <= n/i; i++) 
        if (n % i == 0)
        return false;
  return true;
}

质数判断二分解质因数：

从小到大枚举n的所有因数